
In the branch of
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
known as
Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry: the ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small ...
, the Poncelet–Steiner theorem is one of several results concerning
compass and straightedge
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an ideali ...
constructions having additional restrictions imposed on the traditional rules. This result states that whatever can be constructed by
straightedge
A straightedge or straight edge is a tool used for drawing straight lines, or checking their straightness. If it has equally spaced markings along its length, it is usually called a ruler.
Straightedges are used in the automotive service and ma ...
and
compass
A compass is a device that shows the cardinal directions used for navigation and geographic orientation. It commonly consists of a magnetized needle or other element, such as a compass card or compass rose, which can pivot to align itself with ...
together can be constructed by straightedge alone, provided that a single
circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
and its
centre
Center or centre may refer to:
Mathematics
*Center (geometry), the middle of an object
* Center (algebra), used in various contexts
** Center (group theory)
** Center (ring theory)
* Graph center, the set of all vertices of minimum eccentricity ...
are given. This theorem is related to the rusty compass equivalence.
: ''Any Euclidean construction, insofar as the given and required elements are points (or lines), if it can be completed with both the compass and the straightedge together, may be completed with the straightedge alone provided that no fewer than one circle with its center exist in the plane.''
Though a compass can make constructions significantly easier, it is implied that there is no functional purpose of the compass once the first circle has been drawn. All constructions remain possible, though it is naturally understood that circles and their
arcs cannot be drawn without the compass. This means only that the compass may be used for
aesthetic
Aesthetics, or esthetics, is a branch of philosophy that deals with the nature of beauty and taste, as well as the philosophy of art (its own area of philosophy that comes out of aesthetics). It examines aesthetic values, often expressed th ...
purposes, rather than for the purposes of construction. All points that uniquely define a construction, which can be determined with the use of the compass, are equally determinable without.
Constructions carried out in adherence with this theorem - relying solely on the use of a straightedge tool without the aid of a compass - are known as Steiner constructions. Steiner constructions may involve any number of circles, including none, already drawn in the plane, with or without their centers.
History

In the tenth century, the Persian mathematician
Abu al-Wafa' Buzjani
Abū al-Wafāʾ, Muḥammad ibn Muḥammad ibn Yaḥyā ibn Ismāʿīl ibn al-ʿAbbās al-Būzjānī or Abū al-Wafā Būzhjānī ( fa, ابوالوفا بوزجانی or بوژگانی) (10 June 940 – 15 July 998) was a Persian mathematician ...
(940−998) considered geometric constructions using a straightedge and a compass with a fixed opening, a so-called ''rusty compass''. Constructions of this type appeared to have some practical significance as they were used by artists
Leonardo da Vinci
Leonardo di ser Piero da Vinci (15 April 14522 May 1519) was an Italian polymath of the High Renaissance who was active as a painter, Drawing, draughtsman, engineer, scientist, theorist, sculptor, and architect. While his fame initially res ...
and
Albrecht Dürer
Albrecht Dürer (; ; hu, Ajtósi Adalbert; 21 May 1471 – 6 April 1528),Müller, Peter O. (1993) ''Substantiv-Derivation in Den Schriften Albrecht Dürers'', Walter de Gruyter. . sometimes spelled in English as Durer (without an umlaut) or Due ...
in Europe in the late fifteenth century. A new viewpoint developed in the mid sixteenth century when the size of the opening was considered fixed but arbitrary and the question of how many of Euclid's constructions could be obtained was paramount.
Renaissance
The Renaissance ( , ) , from , with the same meanings. is a period in European history marking the transition from the Middle Ages to modernity and covering the 15th and 16th centuries, characterized by an effort to revive and surpass ideas ...
mathematician
Lodovico Ferrari
Lodovico de Ferrari (2 February 1522 – 5 October 1565) was an Italian mathematician.
Biography
Born in Bologna, Lodovico's grandfather, Bartolomeo Ferrari, was forced out of Milan to Bologna. Lodovico settled in Bologna, and he began his ...
, a student of
Gerolamo Cardano
Gerolamo Cardano (; also Girolamo or Geronimo; french: link=no, Jérôme Cardan; la, Hieronymus Cardanus; 24 September 1501– 21 September 1576) was an Italian polymath, whose interests and proficiencies ranged through those of mathematician, ...
in a "mathematical challenge" against
Niccolò Fontana Tartaglia
Niccolò Fontana Tartaglia (; 1499/1500 – 13 December 1557) was an Italian mathematician, engineer (designing fortifications), a surveyor (of topography, seeking the best means of defense or offense) and a bookkeeper from the then Republi ...
was able to show that "all of Euclid" (that is, the straightedge and compass constructions in the first six books of
Euclid's Elements
The ''Elements'' ( grc, Στοιχεῖα ''Stoikheîa'') is a mathematical treatise consisting of 13 books attributed to the ancient Greek mathematician Euclid in Alexandria, Ptolemaic Egypt 300 BC. It is a collection of definitions, postulat ...
) could be accomplished with a straightedge and rusty compass. Within ten years additional sets of solutions were obtained by Cardano, Tartaglia and Tartaglia's student Benedetti. During the next century these solutions were generally forgotten until, in 1673,
Georg Mohr
Jørgen Mohr (Latinised ''Georg(ius) Mohr''; 1 April 1640 – 26 January 1697) was a Danish mathematician, known for being the first to prove the Mohr–Mascheroni theorem, which states that any geometric construction which can be done with comp ...
published (anonymously and in Dutch) ''Euclidis Curiosi'' containing his own solutions. Mohr had only heard about the existence of the earlier results and this led him to work on the problem.
Showing that "all of Euclid" could be performed with straightedge and rusty compass is not the same as proving that ''all'' straightedge and compass constructions could be done with a straightedge and just a rusty compass. Such a proof would require the formalization of what a straightedge and compass could construct. This groundwork was provided by
Jean Victor Poncelet in 1822, having been motivated by Mohr's work on the
Mohr-Mascheroni theorem. He also conjectured and suggested a possible proof that a straightedge and rusty compass would be equivalent to a straightedge and compass, and moreover, the rusty compass need only be used once. The result that a straightedge and single circle with given centre is equivalent to a straightedge and compass was proved by
Jakob Steiner
Jakob Steiner (18 March 1796 – 1 April 1863) was a Swiss mathematician who worked primarily in geometry.
Life
Steiner was born in the village of Utzenstorf, Canton of Bern. At 18, he became a pupil of Heinrich Pestalozzi and afterwards st ...
in 1833.
[
]
Relationships to other constructs
Various other notions, tools, terminology, etc., is often associated (sometimes loosely) to the Poncelet-Steiner theorem. Some are listed here.
Rusty compass
The rusty compass describes a compass whose hinge is so rusted as to be fused such that its legs - the needle and pencil - are unable to adjust width. In essence, it is a compass whose distance is fixed, and which draws circles of a predetermined and constant, but arbitrary radius. Circles may be drawn centered at any arbitrary point, but the radius is unchangeable.
As a restricted construction paradigm, the ''rusty compass constructions'' allow the use of a straightedge and the fixed-width compass.
In some sense, the rusty compass is a generalization and simplification of the Poncelet-Steiner theorem. Though not more powerful, it is certainly more convenient. The Poncelet-Steiner theorem requires a single circle with arbitrary radius and center point to be placed in the plane. As it is the only drawn circle, whether or not it was drawn by a rusty compass is immaterial and equivalent. The benefit of general rusty compass constructions, however, is that the compass may be used repeatedly to redraw circles centered at any desired point, albeit with the same radius, thus simplifying many constructions. Naturally if all constructions are possible with a single circle arbitrarily placed in the plane, then the same can surely be said about a straightedge and rusty compass.
It is known that a straightedge and a rusty compass is sufficient to construct all that is possible with straightedge and standard compass - with the implied understanding that circular arcs of arbitrary radii cannot be drawn, and only need be drawn for aesthetic purposes rather than constructive ones. Historically this was proven when the Poncelet-Steiner theorem was proven, which is a stronger result. The rusty compass, therefore, is no weaker than the Poncelet-Steiner theorem. The rusty compass is also no stronger.
The Poncelet-Steiner theorem reduces Ferrari's rusty compass equivalence, a claim at the time, to a single-use compass: ''all points necessary to uniquely describe any compass-straightedge construction may be achieved with only a straightedge, once the first circle has been placed.'' The Poncelet-Steiner theorem takes the rusty compass scenario, and breaks the compass completely after its first use.
Steiner constructions
The term Steiner construction typically refers to any geometric construction that utilizes the straightedge tool only, and is sometimes simply called a ''straightedge-only construction''. No stipulations are made about what geometric objects already exist in the plane, and no implications are made about what is or is not possible to construct. Thus, all constructions adhering to the Poncelet-Steiner theorem are Steiner constructions, though not all Steiner constructions adhere to the standard of providing only one circle with its center. The Poncelet-Steiner theorem does not require an actual compass - it is presumed that the circle preexists in the plane - therefore all constructions are Steiner constructions.
Steiner's theorem, a lemma
If only one circle is to be given and no other special information, Steiner's theorem implies that the center of the circle must be provided along with the circle. This is done by
proving the impossibility of constructing the circle's center from straightedge alone using only a single circle in the plane, without its center. An argument using
projective transformations
In projective geometry, a homography is an isomorphism of projective spaces, induced by an isomorphism of the vector spaces from which the projective spaces derive. It is a bijection that maps lines to lines, and thus a collineation. In general, s ...
and
Steiner's conic sections is used.
A naïve summary of the proof is as follows. With the use of a straightedge tool, only linear projective transformations are possible, and linear projective transformations are reversible operations. Lines project onto lines under any linear projective transformation, while conic sections project onto conic sections under a linear projective transformation, but the latter are skewed such that
eccentricities,
foci
Focus, or its plural form foci may refer to:
Arts
* Focus or Focus Festival, former name of the Adelaide Fringe arts festival in South Australia Film
*''Focus'', a 1962 TV film starring James Whitmore
* ''Focus'' (2001 film), a 2001 film based ...
, and centers of circles are not preserved. Under different mappings the center does not map
uniquely and reversibly. This would not be the case if lines could be used to determine a circles center. As linear transformations are reversible operations and would thus produce unique results, the fact that unique results are not possible implies the impossibility of center-point constructions. The uniqueness of the constructed center would depend on additional information which makes the construction reversible.
Thus it is not possible to construct everything that can be constructed with straightedge and compass with straightedge alone. Consequently, requirements on the Poncelet-Steiner theorem cannot be weakened with respect to the circle center. If the centre of the only given circle is not provided, it cannot be obtained by a straightedge alone. Many constructions are impossible with straightedge alone. Something more is necessary, and a circle with its center identified is sufficient.
Alternatively, the center may be omitted with sufficient additional information. This is not a weakening of the Poncelet-Steiner theorem, merely an alternative framework. Nor is it a contradiction of Steiner's Theorem which hypothesizes only a single circle. The inclusion of this sufficient alternative information disambiguates the mappings under the projective transformations, thus allowing various Steiner constructions to recover the circle center. Some alternatives include two
concentric
In geometry, two or more objects are said to be concentric, coaxal, or coaxial when they share the same center or axis. Circles, regular polygons and regular polyhedra, and spheres may be concentric to one another (sharing the same center point ...
or two intersecting circles, or three circles, or
other variations wherein the provided circle(s) are devoid of their centers, but some other unique but sufficient criterion is met. In any of these cases, the center of a circle can be constructed, thereby reducing the problem to the Poncelet-Steiner theorem hypothesis (with the added convenience of having additional circles in the plane).
Constructive proof approach
To prove the theorem, each of the
basic constructions of compass and straightedge need to be proven to be possible by using a straightedge alone (provided that a circle and its center exist in the plane), as these are the foundations of, or elementary steps for, all other constructions. That is to say, all constructions can be written as a series of steps involving these five basic constructions:
#Creating the line through two existing points
#Creating the circle through one point with centre another point
#Creating the point which is the intersection of two existing, non-parallel lines
#Creating the one or two points in the intersection of a line and a circle (if they intersect)
#Creating the one or two points in the intersection of two circles (if they intersect).
#1 - A line through two points
This can be done with a straightedge alone. Neither a compass nor a circle is required.
#2 - A circle through one point with defined center
It is understood that the arc of a circle cannot be drawn without a compass. A circle is considered to be given by any two points, one defining the center and one existing on the
circumference
In geometry, the circumference (from Latin ''circumferens'', meaning "carrying around") is the perimeter of a circle or ellipse. That is, the circumference would be the arc length of the circle, as if it were opened up and straightened out to ...
at radius. Any such pair define a unique circle. In keeping with the intent of the theorem which we aim to prove, the actual circle need not be drawn but for aesthetic reasons.
#3 – Intersection of two lines
This construction can also be done directly with a straightedge.
#4, #5 - The other constructions
Thus, to prove the theorem, only constructions #4 and #5 need be proven possible using only a straightedge and a given circle with its center.
Notes
Any doubts about constructions #1 or #3 would apply equally to the traditional construction paradigm involving the compass, and thus are not concerns unique to the Poncelet-Steiner theorem.
Construction #2 should not be of concern. The arc of the circle is only used in traditional construction paradigms for the purposes of circle-circle and circle-line intersections, thus if constructions #4 and #5 are satisfiable without the arc of the circle, then this will prove non-necessity of drawing the arc. This therefore proves that construction #2 is satisfied by a simple labeling of two points uniquely identifying the circle.
Constructive proof
In general constructions there are often several variations that will produce the same result. The choices made in such a variant can be made without loss of generality. However, when a construction is being used to prove that something can be done, it is not necessary to describe all these various choices and, for the sake of clarity of exposition, only one variant will be given below. The variants below are chosen for their ubiquity in application rather than simplicity under any particular set of special conditions.
In the constructions below, a circle defined by a center point and a point on its circumference, , through which the arc of the circle passes, is denoted . As most circles are not compass-drawn, center and circumference points are named explicitly, and usually separately. Per the theorem, when a compass-drawn circle is provided it is simply referred to as the ''given circle'' or the ''provided circle''. The provided circle should always be assumed to be placed arbitrarily in the plane with an arbitrary radius (i.e. in
general position
In algebraic geometry and computational geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the ''general case'' situation, as opposed to some more special or coincidental cases that ar ...
).
The intersection points between any line and the given circle may be found directly. The Poncelet-Steiner Theorem does not prohibit the normal treatment of circles already drawn in the plane; normal construction rules apply. The theorem only prohibits the construction of new circular arcs with a compass.
It is important to note that Steiner constructions and those constructions herein proving the Poncelet-Steiner theorem require the arbitrary placement of points in space. In some construction paradigms - such as in the geometric definition of the
constructible number
In geometry and algebra, a real number r is constructible if and only if, given a line segment of unit length, a line segment of length , r, can be constructed with compass and straightedge in a finite number of steps. Equivalently, r is con ...
- this may be prohibited.
Some preliminary constructions
To prove the above constructions #4 and #5, which are included below, a few necessary intermediary constructions are also explained below since they are used and referenced frequently. These are also straightedge-only constructions. All constructions below rely on basic constructions #1,#2,#3, and any other construction that is listed prior to it.
Parallel of a line having a collinear bisected segment

This construction does not require the use of the given circle. Naturally any line that passes through the center of the given circle implicitly has a
bisected segment: the
diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for ...
is bisected by the center. The animated gif file embedded at the introduction to this article demonstrates this construction, reiterated here without the circle and with enumerated steps.
Given an arbitrary line (in black) on which there exist two points and , having a
midpoint
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
Formula
The midpoint of a segment in ''n''-dimens ...
between them, and an arbitrary point in the plane (assumed not to be on line ) through which a
parallel
Parallel is a geometric term of location which may refer to:
Computing
* Parallel algorithm
* Parallel computing
* Parallel metaheuristic
* Parallel (software), a UNIX utility for running programs in parallel
* Parallel Sysplex, a cluster of IBM ...
of line is to be made:
# Construct a line (in red).
# Construct a line (in orange).
# Define an arbitrary point on line .
# Construct a line (in green).
# Construct a line (in light blue).
# Lines and intersect at point .
# Construct a line (in purple).
# Lines and intersect at point .
# Construct a line (in dark blue), the desired parallel.
In some literature the bisected line segment is sometimes viewed as a one-dimensional "circle" existing on the line. Alternatively, some literature views the bisected line segment as a two dimensional circle in three dimensional space with the line passing through a diameter, but not parallel to the plane, thus intersecting the plane of construction at two points on the circumference with the midpoint simply being the prescribed circle center.
Creating a bisected segment on a line
If the line passes through the center of a circle, the segment defined by the diameter through the circle is bisected by the center of the circle. In the general case, however, any other line in the plane may have a bisected segment constructed onto it. This construction does require the use of the given circle.
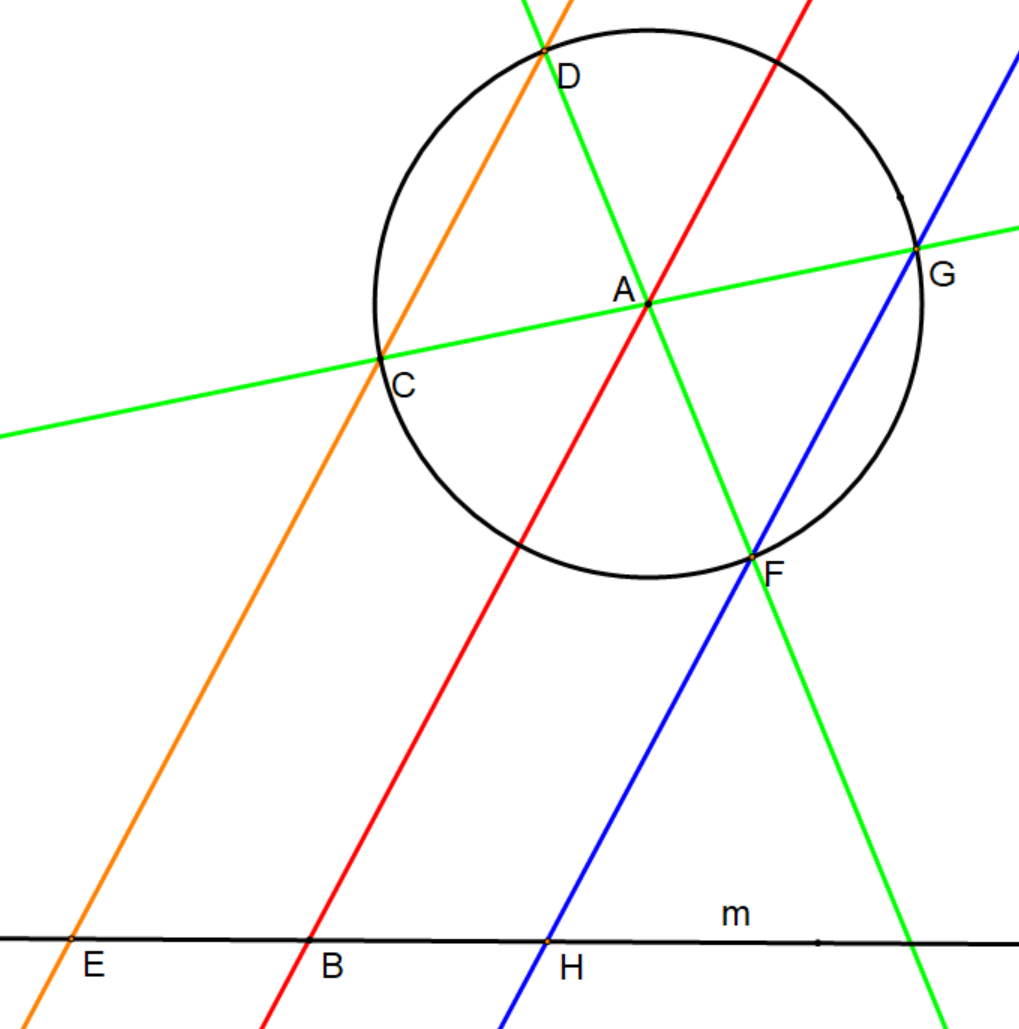
Given a line, (in black), and a circle centered at , we wish to create points , , and on the line such that is the midpoint:
# Draw an arbitrary line (in red) passing through the given circles center, , and the desired midpoint (chosen arbitrarily) on the line .
#* Notice that the red line, , passes through the center of the circle and highlights a diameter, bisected by the circle center. Any parallel may be made from this line according to the previous construction.
# Choose an arbitrary point on the given circle (which does not lie on the perpendicular of through the circle center).
# Construct a line (in orange), passing through , that is parallel to the red line .
#* This parallel intersects the given circle at .
#* This parallel also intersects the black line at , defining one end of the line segment.
# Create two lines (in green), and , that each pass through the given circles center.
#* These green lines intersect the given circle at points and , respectively.
# Line (in blue) intersects the line at , defining the other endpoint of the line segment.
Constructing a parallel of any line
This construction does require the use of the given circle. In order to generalize the parallel line construction to all possible lines, not just the ones with a
collinear
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear (sometimes spelled as colinear). In greater generality, the term has been used for aligned ...
bisected line segment, it becomes necessary to have additional information. In keeping with the Poncelet-Steiner theorem, a circle (with center) is the object of choice for this construction.
To construct a parallel line of any given line, through any point in the plane, we
trivially combine two constructions:
# Any line from which a parallel is to be made must have a bisected segment constructed onto it, if one does not already exist.
# A parallel is then constructed according to the previous parallel construction involving the collinear bisected segment.
In general, however, a parallel may be constructed from any pair of lines which are already parallel to one another; thus a third parallel may be produced from any two, without the use of a circle. Additionally, a parallel of any line may be constructed whenever there exists in the plane any
parallelogram
In Euclidean geometry, a parallelogram is a simple (non- self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equa ...
, also without the use of a given circle.
Constructing a perpendicular line

This construction does require the use of the given circle and takes advantage of
Thales's theorem
In geometry, Thales's theorem states that if A, B, and C are distinct points on a circle where the line is a diameter, the angle ABC is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved ...
.
From a given line , and a given point in the plane, a
perpendicular
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or π/2 radians). The condition of perpendicularity may be represented graphically using the ''perpendicular symbol'', ⟂. It can ...
to the line is to be constructed through the point. Provided is the given circle .
# If the desired line from which a perpendicular is to be made, , does not pass through the given circle (or it also passes through the given circle's center), then a new parallel line (in red) may be constructed arbitrarily such that it does pass through the given circle but not its center, and the perpendicular is to be made from this line instead.
# This red line which passes through the given circle but not its center, will intersect the given circle in two points, and .
# Draw a line , through the circle center.
#* This line intersects the given circle at point .
# Draw a line .
#* This line is perpendicular to the red (and black) lines, and .
# Construct a parallel of line through point using previous constructions.
#* A perpendicular of the original black line, , now exists in the plane, and a parallel of it may be constructed through any point in the plane.
An alternative construction allows a perpendicular to be constructed without the given circle, provided there exists in the plane any
square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
.
Constructing the midpoint of any segment
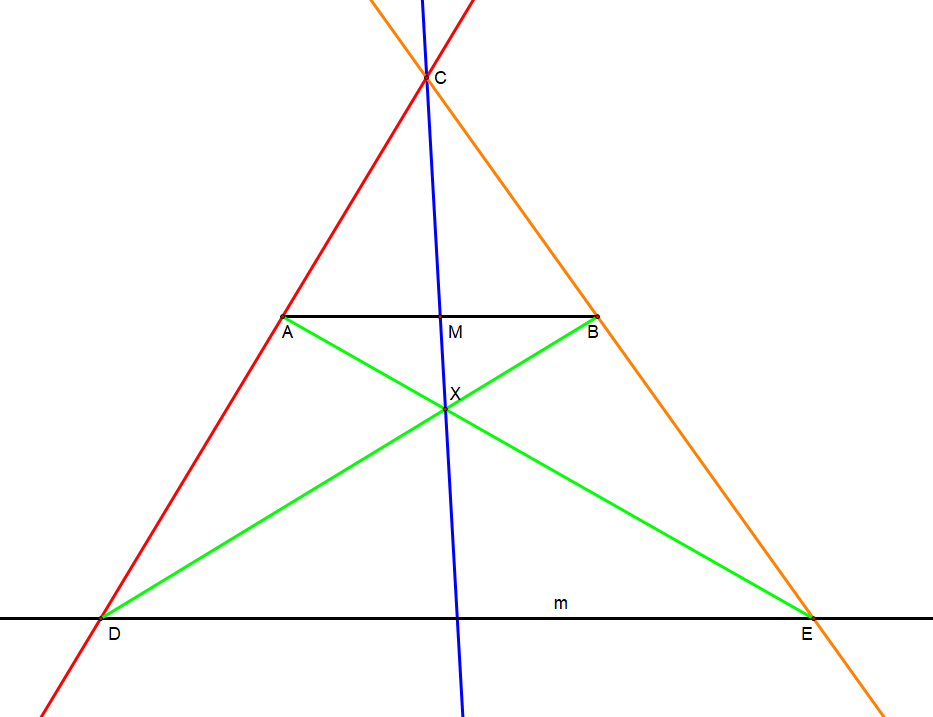
Given is a line segment , which is to be bisected. Optionally, a parallel line exists in the plane.
# If the line , which is parallel to line segment , does not exist in the plane then it must be constructed according to earlier constructions using the given circle in the plane (not depicted).
#* A given circle in the plane is not required for this construction if the parallel already exists.
#* The parallel may be placed in the plane arbitrarily, so long as it is not collinear with the line segment.
# Arbitrarily choose a point in the plane which is not collinear with the line or the line segment.
# Draw a line (in red), intersecting line at point .
# Draw a line (in orange), intersecting line at point .
# Draw two lines, and (each in light green), intersecting each other at point
# Draw a line (in blue), intersecting segment at point .
#* Point is the desired midpoint of segment .
#* Line also bisects segment
For added perspective, in some sense this construction is a variant of a previous construction of a parallel from a bisected line segment. It is the same set of lines when taken on whole, but constructed in a different order, and from a different initial set of conditions, arriving at a different end goal.
Constructing the radical axis between circles

This construction does require the use of the given circle (which is not depicted) for the referenced sub-constructions.
Suppose two circles and are implicitly given, defined only by the points , , , and in the plane, with their centers defined, but are not compass-constructed. The
radical axis
In Euclidean geometry, the radical axis of two non-concentric circles is the set of points whose Power of a point, power with respect to the circles are equal. For this reason the radical axis is also called the power line or power bisector of ...
, line , between the two circles may be constructed:
# Draw a line (in orange) through the circle centers.
# Draw a line segment (in red) between the points on the circumference of the circles.
# Find the midpoint, , of segment .
# Draw lines and (both in light green), connecting the segment midpoint with each of the circle centers.
# Construct a line (in purple) passing through point , and perpendicular to .
# Construct a line (in dark green) passing through point , and perpendicular to .
# Lines and intersect at point .
#* If the lines and are parallel then the segment midpoint is on the line , and the construction will fail. An alternative approach is required (see below).
# Construct a line (in dark blue) perpendicular to line and passing through point .
# Line is the desired radical axis.
= Resolution of failed construction
=
In the event that the construction of the radical axis fails due to there not being an intersection point between parallel lines and , which results from the coincidental placement of the midpoint on the line , an alternative approach is required. One such alternative is given below with the arbitrarily chosen circle used for demonstration, along with the provided circle . The circle of the radical axis construction is not depicted.
To define a circle only the center and one point - any point - on the circumference is required. In principle a new point is constructed such that circle is equal to circle , but point is not equal to point . In essence, segment is rotated to , for a different set of defining points for the same circle. The construction of the radical axis is begun anew with circle standing in for circle . In this way the coincidental placement of the midpoint (now of segment ) on the line is avoided.

One way of going about this which satisfies most conditions is to construct point
diametrically opposite
In mathematics, antipodal points of a sphere are those diametrically opposite to each other (the specific qualities of such a definition are that a line drawn from the one to the other passes through the center of the sphere so forms a true d ...
, collinear with a line :
# Draw the line (in red).
# Construct a parallel (in orange) of line through the center, point , of the given circle.
#* The parallel intersects the given circle at points and .
# Draw a line (in green), connecting the center of circle with the center of the given circle.
# Draw a line (in pink), connecting the points on the circle circumferences.
#* In the general case, points and may be switched
without loss of generality
''Without loss of generality'' (often abbreviated to WOLOG, WLOG or w.l.o.g.; less commonly stated as ''without any loss of generality'' or ''with no loss of generality'') is a frequently used expression in mathematics. The term is used to indicate ...
.
# Lines and intersect in a point .
#* If point does not exist due to lines and being parallel - caused by circles and having equal radii - then refer to step 4 and switch the roles of points and .
# Draw a line (in blue).
# Lines and intersect at a point .
#* Point is the desired point.
In the general case it is now possible to construct the radical axis between the circles = and .
This specific construction of a diametrically opposite point, however, can itself potentially fail under the right conditions - when points , , and are collinear. If the final goal is to construct a diametrically opposite point, an alternative approach is required.
If the goal is to resolve the limitation in the radical axis construction, one option is to attempt a similar construction on circle instead. This too may fail, if all five points are collinear. Alternatively an entirely different point may be determined, not necessarily a diametrically opposite one, requiring a small variation on the above construction.
Intersecting a line with a circle (Construction #4)
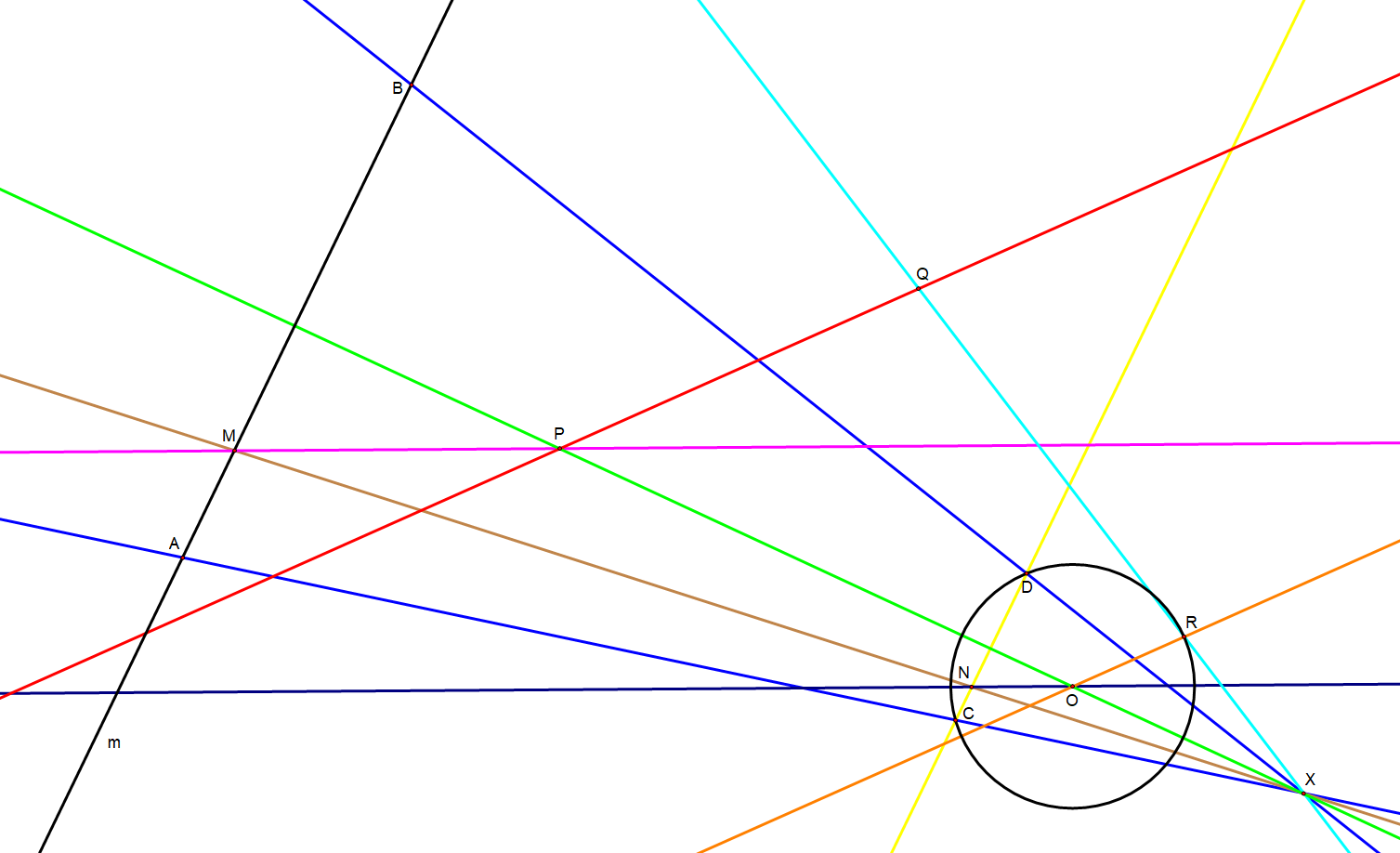
This construction does require the use of the provided circle, .
Given is the line (in black) and the circle , which is not compass-constructed. The intersection points of the circle and the line , which are point and , may be constructed:
# Draw a line (in red) through the points defining the circle.
# Construct a parallel (in orange) of line through the center of the provided circle.
#* The parallel intersects the provided circle at two points, one of which is arbitrarily chosen: .
# Draw a line (in light green), through the centers of the two circles (i.e. the one provided by compass construction and the one which is to be intersected).
# Draw a line (in light blue), connecting the two points on the circumferences of the two circles.
# Intersect the lines and at point .
#* If point does not exist due to lines and being parallel - which results from circles and having equal radii - then refer back to step 2 and choose the alternate point of intersection, .
# Choosing a point arbitrarily on line , such that it is not on line , draw a line (in pink).
#* For construction simplicity and only if line is not parallel to line , lines and may be coincident.
# Draw a line (in brown).
# Construct a parallel (in dark purple) of line through the center of the provided circle.
#* The parallel intersects the line at a point .
# Construct a parallel (in yellow) of line through the point .
#* The parallel intersects the provided circle at points and .
#* If the parallel does not intersect the provided circle then neither does the line intersect circle .
# Draw lines and (both in dark blue).
#* These lines both intersect line at points and , respectively.
# Points and are the desired points of intersection between the line and the circle .
Intersecting two circles (Construction #5)
The intersection between two circles becomes a trivial combination of two earlier constructions:
# Construct the radical axis between the two circles.
# Construct the intersection points between the radical axis (which is a line) and either one of the two circles arbitrarily chosen, using basic construction #4.
# These points are the desired points of intersection of the circles.
#* The two circles and the radical axis all intersect at the same loci of points: two points, one point if tangential, or none if they do not intersect.
#* If the radical axis does not intersect one circle then it intersects neither, and neither do the two circles intersect.
Conclusion
The second basic construction - defining a circle with two points - never needed an arc to be constructed with the compass in order for the circle to be utilized in constructions - namely the intersections with circles and with lines which, together, are the essence of all constructions involving a circle. Thus defining a circle by its center and by any arbitrary point on its circumference is sufficient to fully describe the entire circle and construct with it. Basic construction #2 is satisfied.
Since all five basic constructions have been shown to be achievable with only a straightedge, provided that a single circle with its center is placed in the plane, this proves the Poncelet-Steiner theorem.
Other types of restricted construction
The Poncelet–Steiner theorem can be contrasted with the
Mohr–Mascheroni theorem
In mathematics, the Mohr–Mascheroni theorem states that any geometric construction that can be performed by a compass and straightedge can be performed by a compass alone.
It must be understood that by "any geometric construction", we are refer ...
, which states that any compass and straightedge construction can be performed with only a compass.
The rusty compass restriction allows the use of a compass, provided it produces circles of fixed radius. Although the rusty compass constructions were explored since the 10th century, and all of Euclid was shown to be constructable with a rusty compass by the 17th century, the Poncelet-Steiner theorem proves that the rusty compass and straightedge together are more than sufficient for any and all Euclidean construction. Indeed, the rusty compass becomes a tool simplifying constructions over merely the straightedge and single circle. Viewed the other way, the Poncelet-Steiner theorem not only fixes the width of the rusty compass, but ensures that the compass breaks after its first use.
The requirement that one circle with its center provided has been since generalized to include alternative but equally restrictive conditions. In one such alternative, the entire circle is not required at all. In 1904,
Francesco Severi
Francesco Severi (13 April 1879 – 8 December 1961) was an Italian mathematician. He was the chair of the committee on Fields Medal on 1936, at the first delivery.
Severi was born in Arezzo, Italy. He is famous for his contributions to algeb ...
proved that any small arc (of the circle), together with the centre, will suffice. This construction breaks the rusty compass at any point before the first circle is completed, but after it has begun, and still all constructions remain possible. Thus, the conditions hypothesizing the Poncelet-Steiner theorem may indeed be weakened, but only with respect to the completeness of the circular arc, and not, per the Steiner theorem, with respect to the center.
In two other alternatives, the centre may be omitted entirely provided that given are either two concentric circles, or two distinct intersecting circles, of which there are two cases: two intersection points and one intersection point (tangential circles). From any of these scenarios, centres can be constructed, reducing the scenario to the original hypothesis.
Still other variations exist. It suffices to have two non-intersecting circles (without their centres), provided that at least one point is given on either the centerline or on the radical axis of the two circles, or alternatively to have three non-intersecting circles.
Wolfram's Math World
/ref> Once a single center is constructed, the scenario again reduces to the original hypothesis of the Poncelet-Steiner theorem.
Liberated, or neusis, constructions
Instead of restricting the rules of construction, it is of equal interest to study alleviating the rules. Just as geometers have studied what remains possible to construct (and how) when additional restrictions are placed on traditional construction rules - such as compass only, straightedge only, rusty compass, etc. - they have also studied what constructions becomes possible that weren't already when the natural restrictions inherent to traditional construction rules are alleviated. Questions such as "what becomes constructible", "how might it be constructed", "what are the fewest traditional rules to be broken", "what are the simplest tools needed", "which seemingly different tools are equivalent", etc. are asked.
The arbitrary angle is not trisectable using traditional compass and straightedge rules, for example, but the trisection becomes constructible when allowed the additional tool of an ellipse in the plane. Some of the traditional problems such as angle trisection, doubling the cube
Doubling the cube, also known as the Delian problem, is an ancient geometric problem. Given the edge of a cube, the problem requires the construction of the edge of a second cube whose volume is double that of the first. As with the related pro ...
, squaring the circle
Squaring the circle is a problem in geometry first proposed in Greek mathematics. It is the challenge of constructing a square with the area of a circle by using only a finite number of steps with a compass and straightedge. The difficulty ...
, finding cubic roots, etc., have been resolvable using an expanded set of tools. In general, the objects studied to expand the scope of what is constructible have included:
* Non-constructible "auxiliary" curves in the plane - including any of the conic sections
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special ...
, cycloids, lemniscates, limaçons, the Archimedean spiral
The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes. It is the locus corresponding to the locations over time of a point moving away from a fixed point with a con ...
, any of the trisectrices or quadratrices, and others.
* Physical tools other than the compass and straightedge - generally called ''neuseis'' - which include specific tools such as the Tomahawk
A tomahawk is a type of single-handed axe used by the many Indigenous peoples and nations of North America. It traditionally resembles a hatchet with a straight shaft. In pre-colonial times the head was made of stone, bone, or antler, and Europ ...
, markable straightedges and graduated rulers
A ruler, sometimes called a rule, line gauge, or scale, is a device used in geometry and technical drawing, as well as the engineering and construction industries, to measure distances or draw straight lines.
Variants
Rulers have long ...
, right triangular rulers, linkages, ellipsographs, and others.
* Origami, or paper-folding techniques.
The ancient geometers considered the conic sections, and regarded their use as a less pure form of construction, but more pure than the use of neuseis (alternative physical tools) or other unusual curves. The term ''neusis'' or neusis construction
In geometry, the neusis (; ; plural: grc, νεύσεις, neuseis, label=none) is a geometric construction method that was used in antiquity by Greek mathematicians.
Geometric construction
The neusis construction consists of fitting a line e ...
may also refer to a specific tool or method employed by the ancient geometers.
Approximations
Although not a true and rigorous construction (nor considered a neusis construction by normal definitions), it is possible to approximate a construction to a predetermined level of precision using only compass and straightedge, using a reiterative approach. Although each point, line or circle is a valid construction, what it aims to approximate can never truly be achieved. Indeed, using a compass and straightedge alone, if an infinite number of constructive steps are allowed, many more points beyond what is normally constructible become possible, as a convergent process and limiting behavior. For example, an angle trisection may be performed exactly using an infinite sequence of angle bisections. If terminated at some finite point, an accurate approximation of a trisection can be achieved. In traditional construction rules, this is not allowed: a construction must terminate in a finite number of applications of the compass and straightedge, and must produce the desired construction exactly.
See also
*Steel square
The steel square is a tool used in carpentry. Carpenters use various tools to lay out structures that are square (that is, built at accurately measured right angles), many of which are made of steel, but the name ''steel square'' refers to a spec ...
*Constructible polygon
In mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not. There are infinite ...
*Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, pro ...
*Inversive geometry
Inversive activities are processes which self internalise the action concerned. For example, a person who has an Inversive personality internalises his emotions from any exterior source. An inversive heat source would be a heat source where all th ...
*Geometrography In the mathematical field of geometry, geometrography is the study of geometrical constructions. The concepts and methods of geometrography were first expounded by Émile Lemoine (1840–1912), a French civil engineer and a mathematician, in a m ...
Notes
References
*
*
Further reading
*
External links
Jacob Steiner's theorem
at cut-the-knot
Alexander Bogomolny (January 4, 1948 July 7, 2018) was a Soviet-born Israeli-American mathematician. He was Professor Emeritus of Mathematics at the University of Iowa, and formerly research fellow at the Moscow Institute of Electronics and Math ...
(It is impossible to find the center of a given circle with the straightedge alone)
Straightedge alone
Basic constructions of straightedge-only constructions.
Two circles and only a straightedge
an article by Arseniy Akopyan and Roman Fedorov.
A remark on the construction of the centre of a circle by means of the ruler
by Christian Gram.
a page primarily about Steiner's Theorem
Poncelet-Steiner Theorem
{{DEFAULTSORT:Poncelet-Steiner theorem
Euclidean plane geometry
Theorems in plane geometry
Compass and straightedge constructions
 In the branch of
In the branch of  In the tenth century, the Persian mathematician
In the tenth century, the Persian mathematician  This construction does not require the use of the given circle. Naturally any line that passes through the center of the given circle implicitly has a bisected segment: the
This construction does not require the use of the given circle. Naturally any line that passes through the center of the given circle implicitly has a bisected segment: the  Given a line, (in black), and a circle centered at , we wish to create points , , and on the line such that is the midpoint:
# Draw an arbitrary line (in red) passing through the given circles center, , and the desired midpoint (chosen arbitrarily) on the line .
#* Notice that the red line, , passes through the center of the circle and highlights a diameter, bisected by the circle center. Any parallel may be made from this line according to the previous construction.
# Choose an arbitrary point on the given circle (which does not lie on the perpendicular of through the circle center).
# Construct a line (in orange), passing through , that is parallel to the red line .
#* This parallel intersects the given circle at .
#* This parallel also intersects the black line at , defining one end of the line segment.
# Create two lines (in green), and , that each pass through the given circles center.
#* These green lines intersect the given circle at points and , respectively.
# Line (in blue) intersects the line at , defining the other endpoint of the line segment.
Given a line, (in black), and a circle centered at , we wish to create points , , and on the line such that is the midpoint:
# Draw an arbitrary line (in red) passing through the given circles center, , and the desired midpoint (chosen arbitrarily) on the line .
#* Notice that the red line, , passes through the center of the circle and highlights a diameter, bisected by the circle center. Any parallel may be made from this line according to the previous construction.
# Choose an arbitrary point on the given circle (which does not lie on the perpendicular of through the circle center).
# Construct a line (in orange), passing through , that is parallel to the red line .
#* This parallel intersects the given circle at .
#* This parallel also intersects the black line at , defining one end of the line segment.
# Create two lines (in green), and , that each pass through the given circles center.
#* These green lines intersect the given circle at points and , respectively.
# Line (in blue) intersects the line at , defining the other endpoint of the line segment.
 This construction does require the use of the given circle and takes advantage of
This construction does require the use of the given circle and takes advantage of  Given is a line segment , which is to be bisected. Optionally, a parallel line exists in the plane.
# If the line , which is parallel to line segment , does not exist in the plane then it must be constructed according to earlier constructions using the given circle in the plane (not depicted).
#* A given circle in the plane is not required for this construction if the parallel already exists.
#* The parallel may be placed in the plane arbitrarily, so long as it is not collinear with the line segment.
# Arbitrarily choose a point in the plane which is not collinear with the line or the line segment.
# Draw a line (in red), intersecting line at point .
# Draw a line (in orange), intersecting line at point .
# Draw two lines, and (each in light green), intersecting each other at point
# Draw a line (in blue), intersecting segment at point .
#* Point is the desired midpoint of segment .
#* Line also bisects segment
For added perspective, in some sense this construction is a variant of a previous construction of a parallel from a bisected line segment. It is the same set of lines when taken on whole, but constructed in a different order, and from a different initial set of conditions, arriving at a different end goal.
Given is a line segment , which is to be bisected. Optionally, a parallel line exists in the plane.
# If the line , which is parallel to line segment , does not exist in the plane then it must be constructed according to earlier constructions using the given circle in the plane (not depicted).
#* A given circle in the plane is not required for this construction if the parallel already exists.
#* The parallel may be placed in the plane arbitrarily, so long as it is not collinear with the line segment.
# Arbitrarily choose a point in the plane which is not collinear with the line or the line segment.
# Draw a line (in red), intersecting line at point .
# Draw a line (in orange), intersecting line at point .
# Draw two lines, and (each in light green), intersecting each other at point
# Draw a line (in blue), intersecting segment at point .
#* Point is the desired midpoint of segment .
#* Line also bisects segment
For added perspective, in some sense this construction is a variant of a previous construction of a parallel from a bisected line segment. It is the same set of lines when taken on whole, but constructed in a different order, and from a different initial set of conditions, arriving at a different end goal.
 This construction does require the use of the given circle (which is not depicted) for the referenced sub-constructions.
Suppose two circles and are implicitly given, defined only by the points , , , and in the plane, with their centers defined, but are not compass-constructed. The
This construction does require the use of the given circle (which is not depicted) for the referenced sub-constructions.
Suppose two circles and are implicitly given, defined only by the points , , , and in the plane, with their centers defined, but are not compass-constructed. The  One way of going about this which satisfies most conditions is to construct point
One way of going about this which satisfies most conditions is to construct point  This construction does require the use of the provided circle, .
Given is the line (in black) and the circle , which is not compass-constructed. The intersection points of the circle and the line , which are point and , may be constructed:
# Draw a line (in red) through the points defining the circle.
# Construct a parallel (in orange) of line through the center of the provided circle.
#* The parallel intersects the provided circle at two points, one of which is arbitrarily chosen: .
# Draw a line (in light green), through the centers of the two circles (i.e. the one provided by compass construction and the one which is to be intersected).
# Draw a line (in light blue), connecting the two points on the circumferences of the two circles.
# Intersect the lines and at point .
#* If point does not exist due to lines and being parallel - which results from circles and having equal radii - then refer back to step 2 and choose the alternate point of intersection, .
# Choosing a point arbitrarily on line , such that it is not on line , draw a line (in pink).
#* For construction simplicity and only if line is not parallel to line , lines and may be coincident.
# Draw a line (in brown).
# Construct a parallel (in dark purple) of line through the center of the provided circle.
#* The parallel intersects the line at a point .
# Construct a parallel (in yellow) of line through the point .
#* The parallel intersects the provided circle at points and .
#* If the parallel does not intersect the provided circle then neither does the line intersect circle .
# Draw lines and (both in dark blue).
#* These lines both intersect line at points and , respectively.
# Points and are the desired points of intersection between the line and the circle .
This construction does require the use of the provided circle, .
Given is the line (in black) and the circle , which is not compass-constructed. The intersection points of the circle and the line , which are point and , may be constructed:
# Draw a line (in red) through the points defining the circle.
# Construct a parallel (in orange) of line through the center of the provided circle.
#* The parallel intersects the provided circle at two points, one of which is arbitrarily chosen: .
# Draw a line (in light green), through the centers of the two circles (i.e. the one provided by compass construction and the one which is to be intersected).
# Draw a line (in light blue), connecting the two points on the circumferences of the two circles.
# Intersect the lines and at point .
#* If point does not exist due to lines and being parallel - which results from circles and having equal radii - then refer back to step 2 and choose the alternate point of intersection, .
# Choosing a point arbitrarily on line , such that it is not on line , draw a line (in pink).
#* For construction simplicity and only if line is not parallel to line , lines and may be coincident.
# Draw a line (in brown).
# Construct a parallel (in dark purple) of line through the center of the provided circle.
#* The parallel intersects the line at a point .
# Construct a parallel (in yellow) of line through the point .
#* The parallel intersects the provided circle at points and .
#* If the parallel does not intersect the provided circle then neither does the line intersect circle .
# Draw lines and (both in dark blue).
#* These lines both intersect line at points and , respectively.
# Points and are the desired points of intersection between the line and the circle .